
Department of Electrical and Computer Engineering
Louisiana State University, Baton Rouge, LA 70803-5901
Email: jxr@ee.lsu.edu
J. Ramanujam
Department of Electrical and Computer Engineering
Louisiana State University, Baton Rouge, LA 70803-5901
Email: jxr@ee.lsu.edu
This paper presents an approach to modeling loop transformations using
linear algebra. Compound transformations are modeled as integer
matrices. Non-singular linear transformations presented here subsumes
the class of unimodular transformations. The loop transformations
included are the unimodular transformations -- reversal, skewing,
permutation -- and a new transformation, namely stretching.
Non-unimodular transformations (with determinant 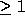 ) create
``holes'' in the transformed iteration space, rendering code
generation difficult. We solve this problem by suitably changing the
step size of loops in order to ``skip'' these holes when traversing
the transformed iteration space. For the class of non-unimodular loop
transformations, we present algorithms for deriving the loop bounds,
the array access expressions and step sizes of loops in the nest.
To derive the step sizes, we compute the Hermite Normal
Form of the transformation matrix; the step sizes are the entries
on the diagonal of this matrix. We then use the theory of Hessenberg
matrices in the derivation of exact loop bounds for non-unimodular
transformations.
We illustrate the use of this approach in several problems
such as generation of tile sets, and distributed memory code generation.
This approach provides a framework for
optimizing programs for a variety of architectures.
) create
``holes'' in the transformed iteration space, rendering code
generation difficult. We solve this problem by suitably changing the
step size of loops in order to ``skip'' these holes when traversing
the transformed iteration space. For the class of non-unimodular loop
transformations, we present algorithms for deriving the loop bounds,
the array access expressions and step sizes of loops in the nest.
To derive the step sizes, we compute the Hermite Normal
Form of the transformation matrix; the step sizes are the entries
on the diagonal of this matrix. We then use the theory of Hessenberg
matrices in the derivation of exact loop bounds for non-unimodular
transformations.
We illustrate the use of this approach in several problems
such as generation of tile sets, and distributed memory code generation.
This approach provides a framework for
optimizing programs for a variety of architectures.
Loop transformations are widely used by automatic parallelizers to generate efficient code for a variety of high performance computers [1,4,20,24]. The interactions among loop transformations is of particular importance for the success of parallelizing compilers. The order of applying a set of transformations has a great impact on the performance of the loop on a given target parallel machine. In addition, it is becoming increasingly common for programmers of highly concurrent machines to specify parallelism using language constructs. Hence, compound loop transformations have received great attention recently.
Banerjee [4], Dowling [6], Wolf and Lam
[19] and this author [14] have derived
unimodular transformations that model compound loop
transformations using integer matrices with unit determinant.
This paper presents an approach for restructuring nested loops
using general non-singular linear transformations, the matrices
associated with which need not have unit determinants.
Non-singular linear
transformations presented here subsumes the class of unimodular
transformations. Non-unimodular transformations (with determinant 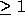 )
create ``holes'' in the transformed iteration space. We change
the step size of loops in order to ``step aside from these holes''
when traversing the transformed iteration space.
For the class of non-unimodular loop transformations,
we present algorithms for deriving the loop bounds, the array
access expressions and step sizes of loops in the nest.
In order to derive the step sizes, we compute the Hermite Normal
Form of the transformation matrix; the step sizes are the entries
on the diagonal of this matrix.
In addition to these advantages, the approach provides a
controlled search of the space of possible loop optimizations.
We illustrate the use of this approach in several problems such
as generation of tile sets, distributed memory code generation and
dependence analysis.
)
create ``holes'' in the transformed iteration space. We change
the step size of loops in order to ``step aside from these holes''
when traversing the transformed iteration space.
For the class of non-unimodular loop transformations,
we present algorithms for deriving the loop bounds, the array
access expressions and step sizes of loops in the nest.
In order to derive the step sizes, we compute the Hermite Normal
Form of the transformation matrix; the step sizes are the entries
on the diagonal of this matrix.
In addition to these advantages, the approach provides a
controlled search of the space of possible loop optimizations.
We illustrate the use of this approach in several problems such
as generation of tile sets, distributed memory code generation and
dependence analysis.
Section 2 presents the terminology and assumptions used in this paper. Section 3 discusses unimodular loop transformations and introduces loop stretching; in addition, we argue that unimodularity is not sufficient for optimizing communication with tiling for distributed memory machines. Issues in code generation for unimodular and non-unimodular transformations are discussed in Section 4. Section 5 presents solutions to the issues of loop step size (based on the Hermite Normal Form of the transformation matrix) and exact loop bound generation (based on Hessenberg matrices), in addition to an example illustrating the use of our techniques. In Section 6, we discuss applications of the Hermite Normal From to such applications as tile set generation, and distributed memory code generation. Section 7 presents a discussion of related work. Section 8 summarizes the paper and points to other applications and work in progress.
A data dependence between two references arises from their
reading or writing a common memory location. This dependence is called
an input dependence if both the references are reads; input
dependences do not constrain program execution ordering. If at least
one of the two references is a write, the dependence can be a flow,
anti or output dependence. Let 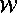 and
and 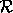 be two
references to a memory location, and let
be two
references to a memory location, and let 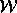 be a write and
be a write and
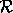 be the read. If
be the read. If 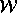 precedes
precedes 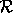 in
sequential execution, then the dependence is called a flow
dependence. If
in
sequential execution, then the dependence is called a flow
dependence. If 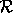 precedes
precedes 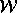 in sequential
execution, then the dependence is called an anti dependence.
If both the accesses to the memory location are writes, we have an
output dependence.
in sequential
execution, then the dependence is called an anti dependence.
If both the accesses to the memory location are writes, we have an
output dependence.
Data dependences are characterized by the dependence distance, which is the number of iterations that separate the sink of the dependence from its source. Dependence directions which represent the sign of the dependence distance are also used to characterize dependences. Dependence distance and direction are represented as vectors called dependence vectors. The elements of the vector read from left to right indicate the dependence from the outermost to the innermost loop. We will use dependence vectors as columns vectors. A dependence matrix has as its columns, a set of dependence vectors. All dependence vectors are positive vectors, i.e., the first non-zero component in the vector (read left to right) must be positive. Any loop transformation is legal if after transformation, the dependence vectors remain positive vectors. A detailed discussion of dependences including dependence testing can be found in [1,3,20,23,24].
The set of computations in a perfectly nested loop is called the
computation domain. For the purpose of this paper, only the
structural information of the nested loop, i.e., the
computation domain and the distance matrix D are needed. With the
assumption on loop bound linearity, the sets of computations
considered are finite convex polyhedra of some iteration space in
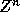 , where n is the number of loops in the nest which is also the
dimensionality of the iteration space. Each element, an iteration of
the loop body S, is referred to by its iteration vector
, where n is the number of loops in the nest which is also the
dimensionality of the iteration space. Each element, an iteration of
the loop body S, is referred to by its iteration vector 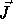 .
.
The iteration set 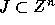 of a given nested loop
is described as a set of integer points (vectors) whose convex hull
of a given nested loop
is described as a set of integer points (vectors) whose convex hull
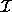 is a non-degenerate (full dimensional) polyhedron, i.e.,
is a non-degenerate (full dimensional) polyhedron, i.e.,
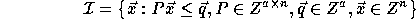
where a is a positive integer and
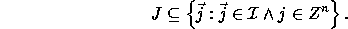
Matrix P is called the constraint matrix of J; vector
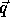 is called the size vector. The above relation simply
states that
is called the size vector. The above relation simply
states that 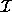 is a polyhedron. Extreme points of polyhedron
is a polyhedron. Extreme points of polyhedron
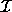 are always integers and belong to the iteration space J
because
are always integers and belong to the iteration space J
because 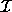 is the convex hull of iteration space J. In
addition, extreme points remain extreme points under rank-preserving
linear transformations. Different size vectors correspond to
instances of the same algorithm that differ only in their sizes (but
have the same shape of the computation domain). The following example
illustrates the concepts introduced here.
is the convex hull of iteration space J. In
addition, extreme points remain extreme points under rank-preserving
linear transformations. Different size vectors correspond to
instances of the same algorithm that differ only in their sizes (but
have the same shape of the computation domain). The following example
illustrates the concepts introduced here.

The computation domain is given by
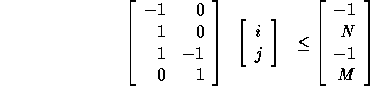
For convenience, we represent the computation domain as the matrix
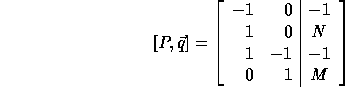
which is just the P matrix augmented with the size vector 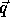 .
.

: Loop transformations: interchange, reversal and
skewing

A distance matrix is a collection of dependence distance vectors for a
nested loop -- the distance vectors are the columns of the distance
matrix. For an n-nested loop with r distance vectors 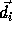
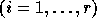 , the distance matrix D is an
, the distance matrix D is an 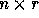 matrix. Let
matrix. Let 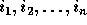 be the loop index variables for
the loop nest levels. The vector
be the loop index variables for
the loop nest levels. The vector 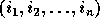 is referred to
as the nest vector.
is referred to
as the nest vector.
Loop transformations are applied to the loop nest vector and the dependence
matrix. Let 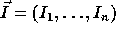 and
and
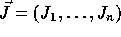 be two iterations of
a nested loop such that
be two iterations of
a nested loop such that 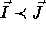 (read
(read 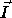 precedes
precedes 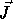 in sequential execution)
and there is
a dependence of constant distance
in sequential execution)
and there is
a dependence of constant distance 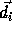 between them.
Applying a linear transformation T to the iteration space (nest vector)
also changes the distance matrix since
between them.
Applying a linear transformation T to the iteration space (nest vector)
also changes the distance matrix since 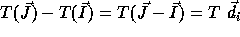 .
All dependence vectors are positive vectors, i.e.,
the first non-zero component should be positive.
We do not include loop-independent dependences which are
zero vectors.
A transformation is legal if the resulting dependence vectors are
still positive vectors [3]. Note that the legality
definition applies to bounded and unbounded sets of dependence vectors;
constant distance vectors are bounded dependence vectors.
Thus, the linear algebraic view
leads to a simpler notion of the legality of a transformation.
For an n-nested sequential loop, the
.
All dependence vectors are positive vectors, i.e.,
the first non-zero component should be positive.
We do not include loop-independent dependences which are
zero vectors.
A transformation is legal if the resulting dependence vectors are
still positive vectors [3]. Note that the legality
definition applies to bounded and unbounded sets of dependence vectors;
constant distance vectors are bounded dependence vectors.
Thus, the linear algebraic view
leads to a simpler notion of the legality of a transformation.
For an n-nested sequential loop, the  identity matrix (
identity matrix (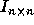 )
denotes sequential execution order.
Loop transformations correspond to elementary row operations on matrices [4].
)
denotes sequential execution order.
Loop transformations correspond to elementary row operations on matrices [4].
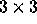 iteration space.
Banerjee [4] showed that
any unimodular transformation can be realized through reversal,
interchange and skewing. In linear algebraic terms, the matrix
associated with a unimodular transformation can be derived by
elementary row operations on an identity matrix [14].
Let
iteration space.
Banerjee [4] showed that
any unimodular transformation can be realized through reversal,
interchange and skewing. In linear algebraic terms, the matrix
associated with a unimodular transformation can be derived by
elementary row operations on an identity matrix [14].
Let 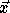 denote the nest vector of a loop nest. Let T denote a
unimodular transformation which results in the transformed nest vector
denote the nest vector of a loop nest. Let T denote a
unimodular transformation which results in the transformed nest vector
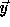 , i.e.,
, i.e., 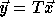 .
A computation domain
.
A computation domain 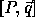 on tranformation T becomes
on tranformation T becomes
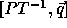 , since
, since 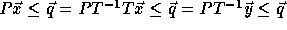 .
.

: Effect of unimodularity of communication
Loop stretching is a transformation that corresponds to changing the step size of a loop by an integer factor f. Stretching is always legal since it does not alter the order of execution. Loop stretching is the inverse of loop step normalization [20,24]. Multiplying a row by f where f > 1 corresponds to stretching. For example, the transformation,

changes the step size of the inner loop to 2. Figure 2
illustrates the effect of T on a 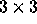 iteration space. Note
that within the boundary of the transformed iteration space, there
are points which are skipped over; we refer to these points as ``holes.''
These are the points in the transformed iteration space which are
not images of any point in the original iteration space, i.e.,
these
are vectors
iteration space. Note
that within the boundary of the transformed iteration space, there
are points which are skipped over; we refer to these points as ``holes.''
These are the points in the transformed iteration space which are
not images of any point in the original iteration space, i.e.,
these
are vectors 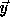 for which
for which 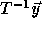 is not integral.
is not integral.
Any nonsingular integer linear transformation can be realized through combinations of reversal, stretching, interchange and skewing -- this follows from the fact that a series of row operations applied to the identity matrix can generate any integer matrix [18].
In this section, we present an example to show the need for
non-unimodular transformations. Iteration space tiling
[9,13,16,19,20,21] is
a transformation that decomposes an n-dimensional iteration
space into n-dimensional ``blocks'' composed of a number of iterations
where each block executes atomically; hence there should be no
dependence cycles (deadlock) among the blocks.
Tiling is extremely useful in distributed memory
machines and hierarchical shared memory machines in exploiting
locality of reference in the presence of dependences
[13,16,17].
In [16], we modeled the problem of finding the best
tiling transformation for distributed memory machines as (a linear
programming problem) that
of finding a matrix T such that the entries in
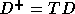 are non-negative (so that
there are no dependence cycles) and the sum of the entries in
are non-negative (so that
there are no dependence cycles) and the sum of the entries in 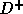 is a minimum; the sum of the entries in
is a minimum; the sum of the entries in 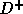 corresponds to the
amount of communication (flux or volume) required.
In 2-dimensional iteration spaces,
the best transformation matrix is not necessarily unimodular
[13]. For example, consider the distance matrix
corresponds to the
amount of communication (flux or volume) required.
In 2-dimensional iteration spaces,
the best transformation matrix is not necessarily unimodular
[13]. For example, consider the distance matrix
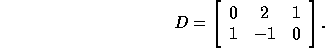
The tiling transformation T with the least communication is

whose determinant is 2. From a transformational view, we need to find a non-singular matrix T

such that
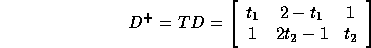
has nonnegative entries. The optimal solutions for linear programming problems
occur at the simplex vertices or corners of the feasible region.
The corners of the feasible region for the above set of constraints are:
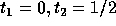 and
and 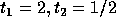 .
Since we require that T is non-singular,
its determinant must be nonzero i.e.,
.
Since we require that T is non-singular,
its determinant must be nonzero i.e., 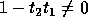 , the second
simplex point
, the second
simplex point 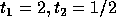 cannot be considered. Therefore, the solution is
cannot be considered. Therefore, the solution is
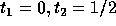 . In general, we need to consider only those simplex vertices
where the matrix T would be non-singular.
Among unimodular matrices of the form
. In general, we need to consider only those simplex vertices
where the matrix T would be non-singular.
Among unimodular matrices of the form

a=1 gives the minimum communication volume. If we look for non-singular matrices of the form

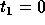 and
and 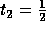 gives the smallest communication volume.
Figure 3 illustrates the effect of unimodularity on
communication. In Figure 3, we do not show the communication
arising due to the dependence vector
gives the smallest communication volume.
Figure 3 illustrates the effect of unimodularity on
communication. In Figure 3, we do not show the communication
arising due to the dependence vector 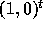 . The tile shape in
Figure 3(a) is generated by the non-unimodular matrix
. The tile shape in
Figure 3(a) is generated by the non-unimodular matrix

and the tile shape shape in Figure 3(b) is generated by the unimodular matrix

We note that T in this case has a determinant 2 and thus can not be generated by unimodular transformations. The reader is referred to [13] for details.
Assume that a unimodular transformation T is applied to a loop nest. The issues in code generation for T are:
Let 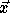 denote the nest vector for the original iteration
space and
denote the nest vector for the original iteration
space and 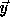 denote the transformed iteration space nest
vector, i.e.,
denote the transformed iteration space nest
vector, i.e., 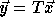 is
the image of
is
the image of 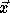 under T.
We assume that the array index expressions are
affine functions of the loop indices
i.e., of the form
under T.
We assume that the array index expressions are
affine functions of the loop indices
i.e., of the form
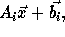 where
where 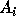 is an
is an 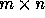 matrix
(assuming that the array being referenced is of dimension m)
and the vector
matrix
(assuming that the array being referenced is of dimension m)
and the vector 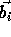 is an m-element vector (referred to
as the offset vector).
We want the same array elements accessed in
is an m-element vector (referred to
as the offset vector).
We want the same array elements accessed in 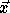 and
and 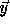 .
Therefore we need
.
Therefore we need 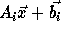 accessed in
accessed in 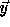 as well. In order to do this, we
change
as well. In order to do this, we
change
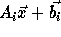 to
to 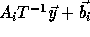 ,
since
,
since 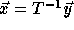 .
.
Specifying a loop involves
writing the values of the upper and lower limits of each loop index
with the constraint that the limit of a loop index 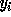
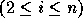 is an affine function of the values of loop indices
is an affine function of the values of loop indices
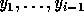 where
where  are the transformed
loop indices.
The computation domain is:
are the transformed
loop indices.
The computation domain is:

Let T be a non-singular transformation applied to the loop nest, then
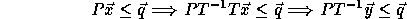
In order to find the new loop bounds:
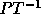 .
.
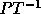 into row echelon form:
into row echelon form:
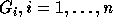 of inequalities -- the ith group of inequalities
consists of all rows of
of inequalities -- the ith group of inequalities
consists of all rows of 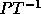 which have a nonzero entry in the
ith column (
which have a nonzero entry in the
ith column (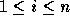 ). The group
). The group 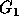 corresponds to
the new outermost loop index,
corresponds to
the new outermost loop index, 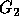 corresponds to the new next loop
index and so on. The groups
corresponds to the new next loop
index and so on. The groups 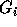 are not disjoint. An inequality (row)
belongs to as many groups as the number of nonzero coefficients in it.
are not disjoint. An inequality (row)
belongs to as many groups as the number of nonzero coefficients in it.
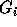 using those in groups
using those in groups 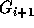 to
to 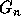 so
that the inequalities in group
so
that the inequalities in group 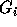 have a coefficient of zero for
have a coefficient of zero for
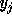
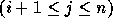 , i.e., all coefficients to the
right of the ith column are zero. This will render
, i.e., all coefficients to the
right of the ith column are zero. This will render 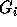 in row echelon form.
in row echelon form.
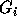 , all inequalities which have a negative
entry in column i give lower bounds and all inequalities with positive
entries in column i give upper bounds for the ith loop in the
transformed nest. The loop lower bound is the
ceiling of the
maximum corresponding to the former while the upper bound is
the floor of the minimum corresponding to the latter.
, all inequalities which have a negative
entry in column i give lower bounds and all inequalities with positive
entries in column i give upper bounds for the ith loop in the
transformed nest. The loop lower bound is the
ceiling of the
maximum corresponding to the former while the upper bound is
the floor of the minimum corresponding to the latter.

: Effect of non-unimodular transformations on
example 1.
In this section, we contrast code generation for non-unimodular transformations with that for unimodular transformation. We use the following loop skeleton to illustrate the application of our techniques:
Consider the following non-unimodular transformation (with determinant 2):

Figure 4 shows the original iteration space and the transformed iteration space for the loop in example 1 under T.
If we generate code in this case as if T were a unimodular transformation, we generate the following incorrect code:
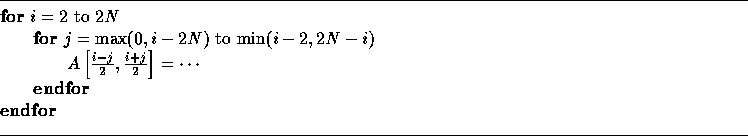
The code generated above traverses all points within the boundary of the transformed iteration space in Figure 4(b). In order for the code to be correct, the step size of the inner loop should be 2 and the bounds of the inner loop have to be corrected. We note here that computation of array index expressions for the transformed nest is the same as with unimodular transformations; therefore, we will not discuss it any further.
The points in the transformed iteration space in Figure 4(b)
that have to be skipped (holes) are those for which there is no corresponding
point in the original iteration space, i.e., points 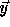 in
the transformed iteration space for which
in
the transformed iteration space for which 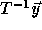 is not integral
are the holes. This suggests the following simple code generation strategy --
in the body of the code generated as if T were unimodular, add a guard
for each iteration as shown below:
is not integral
are the holes. This suggests the following simple code generation strategy --
in the body of the code generated as if T were unimodular, add a guard
for each iteration as shown below:
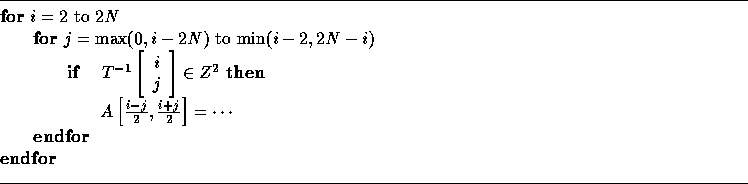
This incurs expensive runtime overhead. In the next section, we show how to generate code which avoids expensive runtime overhead. Thus, the remaining issues in code generation (discussed next) are:
We generalize unimodular transformations described by [4,19]
to derive non-singular linear transformations defined by
integer matrices whose determinant is not restricted to 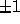 .
This section presents details of code generation for non-unimodular
loop transformations. Iteration spaces defined by nested loops
form bounded integer lattices. The theory presented here is based
on the fact that the lattice generated by the columns of a matrix
T is the same as the lattice generated by the Hermite Normal
Form (defined below) of T. The entries on the diagonal
of the Hermite Normal Form of T give the loop step sizes.
In the case of n-nested loops with step size 1, the iteration
space is a lattice generated by the columns of the
.
This section presents details of code generation for non-unimodular
loop transformations. Iteration spaces defined by nested loops
form bounded integer lattices. The theory presented here is based
on the fact that the lattice generated by the columns of a matrix
T is the same as the lattice generated by the Hermite Normal
Form (defined below) of T. The entries on the diagonal
of the Hermite Normal Form of T give the loop step sizes.
In the case of n-nested loops with step size 1, the iteration
space is a lattice generated by the columns of the 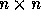 identity matrix
identity matrix 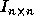 [14], since any point in the iteration
space can be written as integral linear combinations of the columns
of
[14], since any point in the iteration
space can be written as integral linear combinations of the columns
of 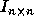 . If the step size along loop level j is
. If the step size along loop level j is 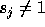 ,
then the corresponding iteration space is generated by
a matrix which differs from
,
then the corresponding iteration space is generated by
a matrix which differs from 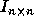 in that the entry
in that the entry 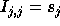 .
.
An 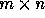 matrix C is unimodular if it is integral and its
determinant is
matrix C is unimodular if it is integral and its
determinant is 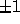 .
The set
.
The set
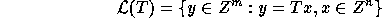
where T is an 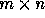 matrix is called the
lattice generated by the columns of T.
matrix is called the
lattice generated by the columns of T.
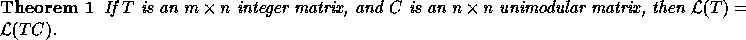
Proof: Let x=Cz. Then we have
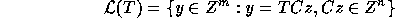
Since C is an integer matrix, 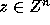 implies
implies
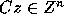 . Since C is unimodular,
. Since C is unimodular, 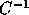 is also
unimodular and integral; hence
is also
unimodular and integral; hence 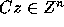 implies that
implies that
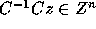 or
or 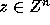 .
Thus, it follows that
.
Thus, it follows that
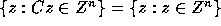 .
Therefore,
.
Therefore, 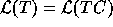 .
.

An 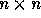 non-singular matrix H is said to be in
Hermite Normal Form if:
non-singular matrix H is said to be in
Hermite Normal Form if:
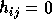 for i < j.
for i < j.
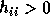 for
for 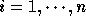 .
.
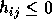 and
and 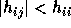 for i>j
for i>j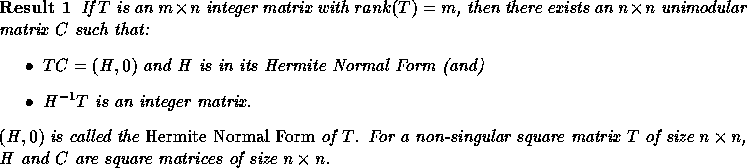
The right multiplication of T by a unimodular matrix C corresponds to a sequence of elementary column operations defined below:
To compute the step sizes, we first compute the Hermite Normal Form, H of the transformation matrix, T. Since the columns of H and T generate the same lattice, the entries on the diagonal of H are the step sizes of the loops in the nest.
In this section, we discuss how to correct the loop bounds generated by using the procedure in Section 4.1.2. For this, we need closed form expressions for the solution of lower triangular matrices. Fortunately, the theory of lower Hessenberg matrices [7] comes to our rescue and allows us to derive closed form solutions for inverting lower triangular matrices. The reader may note that, while the theory of Hessenberg matrices is actually an application of Cramer's rule and determinant expansions, the derived closed form solutions are quite useful in a compiler that implements the transformations.
Every valid point 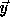 in the transformed iteration space must be
the image of a point
in the transformed iteration space must be
the image of a point 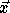 in the original iteration space. This
means that
in the original iteration space. This
means that 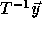 must be integral. Since the columns of the
matrices T and H generate the same lattice, it is sufficient to
check that
must be integral. Since the columns of the
matrices T and H generate the same lattice, it is sufficient to
check that 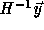 is integral for every point
is integral for every point 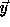 in
the transformed iteration space. These checks are expensive since they
add to runtime overhead. Given that the step sizes are correct, if we
hit the right starting point for each loop, then we generate all and
only the valid points in the transformed iteration space.
in
the transformed iteration space. These checks are expensive since they
add to runtime overhead. Given that the step sizes are correct, if we
hit the right starting point for each loop, then we generate all and
only the valid points in the transformed iteration space.
Consider the problem of solving the linear system 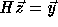 ,
where H is lower triangular. The problem and the solution (
,
where H is lower triangular. The problem and the solution (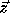 )
are shown below for a
)
are shown below for a 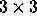 matrix, H.
matrix, H.
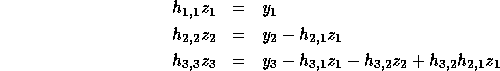
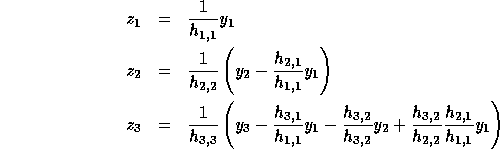
To derive closed form expressions for  , we use determinants of
the Hessenberg matrix M associated with H defined as follows:
, we use determinants of
the Hessenberg matrix M associated with H defined as follows:
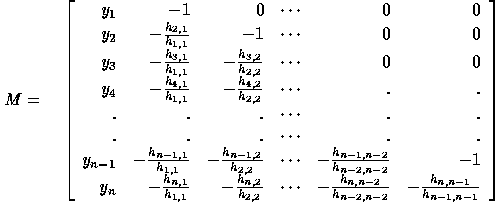
Notice that M is obtained from H by dividing each column in H
by the diagonal element on that column, then changing
the sign of each element of H, dropping its last column, and
adding the vector 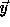 as the new first column. Let
as the new first column. Let 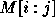 refer to the
sub-matrix of M formed by rows i thru j and columns i thru j where
refer to the
sub-matrix of M formed by rows i thru j and columns i thru j where
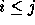 . For example,
. For example,
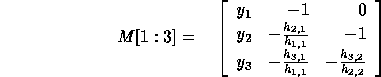
Let 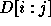 be the determinant of
be the determinant of 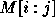 . Thus,
. Thus,
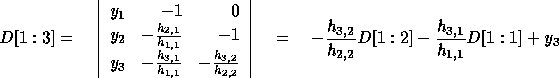
In general,
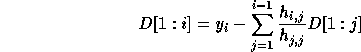
and

Thus, using lower Hessenberg matrices, we have closed form expressions
for 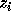 .
.
Let the nest vector for the original iteration space be
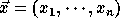 and
and 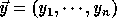 be
the nest vector for the transformed iteration space under T.
Let
be
the nest vector for the transformed iteration space under T.
Let 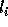 and
and 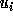
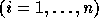 be the lower and upper bounds of the
transformed loops as calculated using the procedure given in
Section 4.1.2.
Since floors and ceilings are used
in computing respectively the lower and upper bounds,
be the lower and upper bounds of the
transformed loops as calculated using the procedure given in
Section 4.1.2.
Since floors and ceilings are used
in computing respectively the lower and upper bounds,
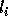 and
and 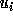 are accurate boundaries of the transformed
iteration space if T were unimodular;
where as the closest integer point computed
using the steps in Section 4.1.2
need not be the image of a point in the source iteration
space. While no point outside the boundary computed as above
belongs to the transformed iteration space, there may be points
inside which do not belong.
In the following discussion, we use
are accurate boundaries of the transformed
iteration space if T were unimodular;
where as the closest integer point computed
using the steps in Section 4.1.2
need not be the image of a point in the source iteration
space. While no point outside the boundary computed as above
belongs to the transformed iteration space, there may be points
inside which do not belong.
In the following discussion, we use 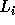 and
and 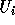 (
(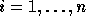 ) to refer to the exact bounds.
) to refer to the exact bounds.
To generate only the valid points in the transformed iteration
space, the loop body of the transformed nest must be
executed only for 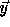 for which
for which
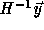 is integral. From the above,
results, it follows that for
is integral. From the above,
results, it follows that for 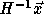 to be integral,
to be integral,
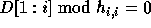 for
for 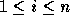 .
We note here the bounds of the outermost loop are always exact, since the image
of a corner of a polyhedron is a corner under invertible linear
transformations. We apply the correction to the loop bounds for
loops
.
We note here the bounds of the outermost loop are always exact, since the image
of a corner of a polyhedron is a corner under invertible linear
transformations. We apply the correction to the loop bounds for
loops 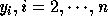 . The basic idea behind the correction is
as follows: if
. The basic idea behind the correction is
as follows: if 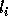 is not exact, then there exists an integer
is not exact, then there exists an integer 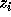 such that
such that 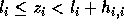 and
and 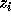 is exact. We need to
find
is exact. We need to
find 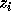 without searching for it. The theory of Hessenberg matrices
comes to our rescue. We use the following modified
form of the Hessenberg matrix:
without searching for it. The theory of Hessenberg matrices
comes to our rescue. We use the following modified
form of the Hessenberg matrix:
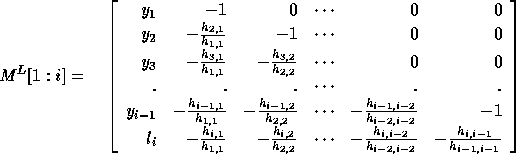
The only difference between 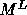 used here and the matrix M in
Section 5.2.1 is that,
we use
used here and the matrix M in
Section 5.2.1 is that,
we use 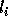 (the loop bound calculated by the procedure in
Section 4.1.2 for loop variable
(the loop bound calculated by the procedure in
Section 4.1.2 for loop variable 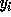 ) instead of
) instead of 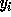 . Let
. Let
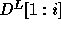 be the determinant of the matrix
be the determinant of the matrix 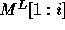 .
. 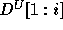 and
and 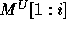 are similarly defined (using
are similarly defined (using 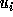 in the place of
in the place of 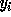 ).
Let
).
Let 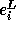 denote the expression
denote the expression 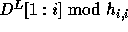 and
and 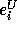 denote the expression
denote the expression 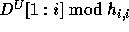 .
If
.
If 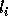 is exact, then
is exact, then 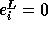 . If
. If
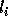 is not exact,
is not exact, 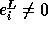 ; hence,
; hence, 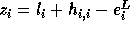 .
Similarly, if
.
Similarly, if 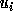 is not exact, then the correct bound is
is not exact, then the correct bound is 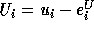 .
Thus, the exact lower bound is given by
.
Thus, the exact lower bound is given by
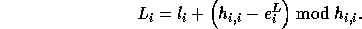
The exact upper bound is

The exact bounds derived here obviate the need for expensive runtime checks used in [2,5,11].
We refer to the loop in Example 1; for convenience, we reproduce the example below:

Consider the following non-unimodular transformation

In order to restructure the loop nest, we first find the HNF of T. The matrix H (the HNF of T) is derived through the following column operation:

Therefore, in the transformed loop nest, the step size of the
outer loop is 1 and the inner loop is 2. The matrix 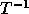 is:
is:
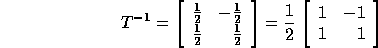
The computation domain (P matrix augmented with vector  ) is:
) is:
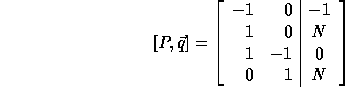
In order to compute the loop bounds, we first compute 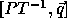 :
:
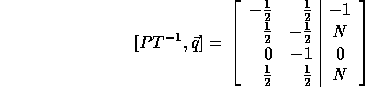
which can be scaled to become:
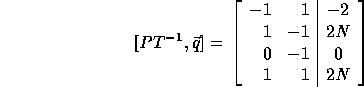
If we replace row 1 by the sum of rows 1 and 3 and if we replace row 2 by the sum of rows 2 and 4, we get the bounds of the outer loop from

Thus, the new outer loop limits are 2 and 2N and the step size is 1. Similarly, we can derive the loop limits of the inner loop whose step size is 2. The (incorrect) inner loop bounds are:
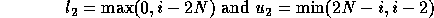
In all cases, the lower bound as calculated is 0.
The 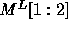 and
and 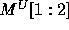 matrices are:
matrices are:

Thus, 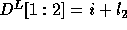 and
and 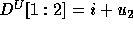 .
Therefore, the corrected loop bounds are:
.
Therefore, the corrected loop bounds are:
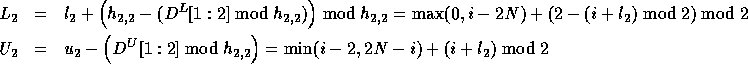
Since 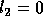 , we can write
, we can write 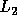 as
as 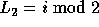 .
The correct transformed code:
.
The correct transformed code:
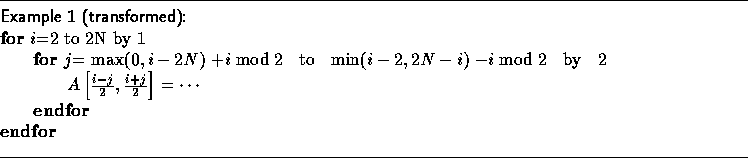
We note here that the correction factor applied to loop bounds follows a regular pattern. In ongoing work [15], we have characterized the sequence of applied correction factors as a finite-state machine that depends on the computed loop step size and the shape of the source iteration space. The use of the finite-state machine reduces runtime overhead.
In tiling a nest of loops, the set of tiles (referred to as the
tile set) is defined as a collection of origins of the tiles.
An origin of a tile, is the lexicographically earliest (smallest) iteration
that belongs to the tile. Hence, the origins of tiles in n-dimensional
iteration spaces
are generated by a matrix whose columns form the basis of the lattice.
In many cases, the lattice of tile origins are defined by a user
through an input matrix or automatically generated by an optimizing
compiler. We use the same terminology as [2] here.
Let L be an 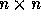 matrix specifying the lattice of
tile origins for a loop nest with a computation domain given
by
matrix specifying the lattice of
tile origins for a loop nest with a computation domain given
by 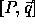 . We show how to generate the origins of the tile sets.
. We show how to generate the origins of the tile sets.
We use the following loop nest (from [2]):

for which tile origins are given by the lattice generated by the columns of L, where L is:

The problem of enumerating tile origins is equivalent to
applying the transformation denoted by the matrix 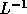 :
:

The computation domain (P matrix augmented with vector 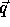 )
is:
)
is:
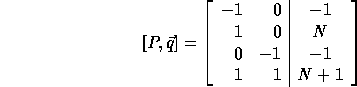
In order to compute the loop bounds, we first compute PL (since
 ).
).
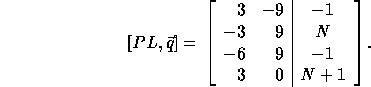
If we replace row 1 by the sum of rows 1 and 3,
we get the bounds of the outer
loop as  and
and 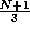 .
Similarly, we can derive the loop bounds of the inner loop.
The loop that traverses the origins of non-empty tiles is:
.
Similarly, we can derive the loop bounds of the inner loop.
The loop that traverses the origins of non-empty tiles is:

If we shift the outer loop to 0, we have:

The points in the transformed iteration space are the origins of non-empty tiles.
Current efforts in distributed memory code generation start with a user-defined decomposition of data structures [8]. Extensions to a serial language allow users to specify the decomposition of arrays. A processor is said to own elements of data allocated to it. The Fortran-D research group at Rice notes: ``We find that selecting a data decomposition is one of the most important intellectual steps in developing data parallel scientific codes'' [8]. The compiler automatically partitions the program using the owner compute rule by which each processor computes values of data it owns. The data owned by a processor is known as its local index set and the set of loop iterations that compute owned data is referred to as the local iteration set [8].
Non-singular transformations may be needed in deriving the local iteration sets; we compute the owner loop bounds so that processors avoid executing expensive guards looking for work to do. Consider the loop shown below:

Assume for this example that the locally owned part of B in
some processor is
given by 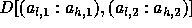 .
The subscript functions can be
represented in matrix form as
.
The subscript functions can be
represented in matrix form as
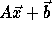 , or
, or
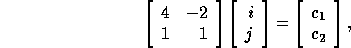
where 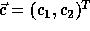 corresponds to a point in the
data space and
corresponds to a point in the
data space and 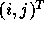 corresponds to a point in the iteration space.
In order to enforce the owner compute
rule,
corresponds to a point in the iteration space.
In order to enforce the owner compute
rule, 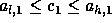 and
and 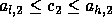 .
That is,
.
That is,


Recall that if the access function is 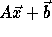 , on applying
a transformation T to the loop, the access function becomes
, on applying
a transformation T to the loop, the access function becomes 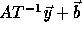 where
where 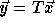 is a vector of the
transformed loop indices. Therefore if a transformation T = A is legal,
the access function becomes
is a vector of the
transformed loop indices. Therefore if a transformation T = A is legal,
the access function becomes 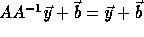 ;
this renders distributed memory code generation easy.
For Example 3,
to generate distributed memory code for this example, we first apply
the transformation T which is the same as the data access function
represented as a matrix:
;
this renders distributed memory code generation easy.
For Example 3,
to generate distributed memory code for this example, we first apply
the transformation T which is the same as the data access function
represented as a matrix:

The Hermite Normal Form of T is

The output generated by our algorithm for T applied to the loop in Example 3 is:

In order to ensure that only local data is accessed, we need to include those in the bounds. We get:

In the following example, we assume that the transformation A (the matrix part of the access function) is not legal and show how to generate code by just adjusting loop bounds. Consider the loop shown below:

Assume for this example that the locally owned part of D in
some processor is
given by 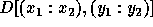 . The subscript functions can be
represented in matrix form as
. The subscript functions can be
represented in matrix form as
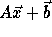 , or
, or
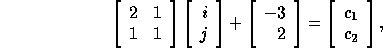
where 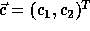 corresponds to a point in the
data space and
corresponds to a point in the
data space and 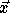 corresponds to a point in the iteration space.
In order to enforce the owner compute
rule,
corresponds to a point in the iteration space.
In order to enforce the owner compute
rule, 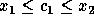 and
and 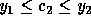 .
That is,
.
That is,


which is equivalent to the following system of inequalities:
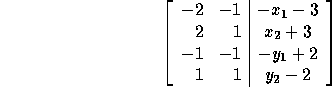
We reduce the above system to row echelon form that results in the following local iteration set for the processor avoiding expensive guards:
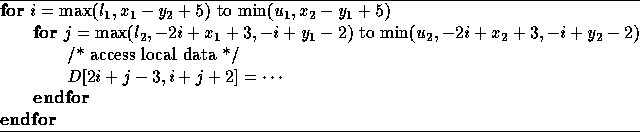
The code generation technique is also applicable for cyclic and block-cyclic forms of data decomposition as well. The Hermite Normal Form is also useful in solving systems of dependence equations which are systems of linear Diophantine equations. It can be used to check if there are no integer solutions; if there are integer solutions, HNF can be used to find a general form of the solutions.
Dowling [6] presents an integer programming solution to the problem of optimal code parallelization using unimodular matrices that transform a given nested loop into parallel form. Banerjee [4] and Wolf and Lam [19] present unimodular transformations of loop nests and algorithms to derive transformations for maximal parallelism. Barnett and Lengauer [5] conclude that unimodularity is not essential; to derive code for non-unimodular transformations, they generate piecewise loop bounds which are not exact. Ancourt and Irigoin [2] and Lu [11] use conditionals in their transformed code to ensure correctness of the transformation. The techniques in this paper obviate the need for such conditionals. The techniques presented in [2,11,5] result in runtime checks. Wolfe [22] presents a technique that searches through a search space comprising both linear and non-linear transformations of the iteration space. In contrast to these approaches, our work presents a theory of non-singular linear transformations of the iteration space characterized by integer matrices whose determinant is an arbitrary integer. We show an example of the need for non-unimodular transformations; the transformations are derived through modifying the step size of the loops. Li and Pingali [10] have independently derived a technique for code generation for general non-singular loop transformations. They present a completion algorithm which given a partial transformation generates a full non-singular transformation matrix that preserves dependences in the loop nest. Their solution decomposes a compound transformation represented by a non-singular matrix into a unimodular transformation followed by a non-unimodular transformation; the second transformation does not change the relative order of execution of iterations. The loop bounds generated involve complex integer operations. In ongoing work [15], we have characterized the sequence of correction factors as a finite-state machine. This reduces the overhead arising from expensive integer operations in loop bound calculations. In addition, their technique does not directly work for applications such as distributed memory code generation.
Compound loop transformations modeled as linear transformations have
received great attention recently. In this paper, we presented a
linear algebraic approach to modeling loop transformations. We
presented techniques for code generation for non-unimodular loop
transformations. Unimodular transformations [4,19] form a
subclass of non-singular linear transformations presented here.
Non-unimodular transformations (with determinant 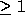 ) create
``holes'' in the transformed iteration space. We change the step size
of loops in order to ``skip'' these holes when traversing the
transformed iteration space. For the class of non-unimodular loop
transformations, we presented algorithms for deriving the loop bounds,
the array access expressions and step sizes of loops in the nest. To
derive the step sizes, we compute the Hermite Normal Form of the
transformation matrix; the step sizes are the entries on the diagonal
of this matrix. We then illustrated the use these techniques in
important applications such as generating tile sets, and deriving
local iteration sets in distributed memory code generation. The
Hermite Normal Form is also useful in dependence analysis. The
technique presented here holds promise in creating a framework for
optimizing programs for a wide variety of architectures.
) create
``holes'' in the transformed iteration space. We change the step size
of loops in order to ``skip'' these holes when traversing the
transformed iteration space. For the class of non-unimodular loop
transformations, we presented algorithms for deriving the loop bounds,
the array access expressions and step sizes of loops in the nest. To
derive the step sizes, we compute the Hermite Normal Form of the
transformation matrix; the step sizes are the entries on the diagonal
of this matrix. We then illustrated the use these techniques in
important applications such as generating tile sets, and deriving
local iteration sets in distributed memory code generation. The
Hermite Normal Form is also useful in dependence analysis. The
technique presented here holds promise in creating a framework for
optimizing programs for a wide variety of architectures.
We thank the anonymous referees for their comments on an earlier draft of the paper.
Beyond Unimodular Transformations
This document was generated using the LaTeX2HTML translator Version 95 (Thu Jan 19 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -t TJS paper -split 0 -no_navigation revised.tex.
The translation was initiated by J. Ramanujam on Fri Mar 3 15:03:11 CST 1995