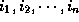 which is
represented by a column vector
which is
represented by a column vector 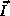 , we define a data reference
matrix,
, we define a data reference
matrix, 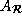 , for each array reference A (distinct or non-distinct)
in a loop nest such that the array reference can be written in the
form
, for each array reference A (distinct or non-distinct)
in a loop nest such that the array reference can be written in the
form 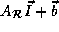 where
where 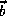 is the offset vector.
is the offset vector.
J. Ramanujam A. Narayan
Department of Electrical and Computer Engineering
Louisiana State University, Baton Rouge, LA 70803-5901
(jxr@ee.lsu.edu)
On a distributed memory machine, local memory accesses are much faster than accesses to non-local data. Inter-processor communication---resulting accesses to non-local data---is a major determinant of the performance of a parallel machine. When a number of non-local accesses are to be made between processors, it is preferable to send fewer but larger messages rather than several smaller messages more frequently (called message vectorization). This is because the message setup cost is usually large. Even in shared memory machines, it is preferable to use block transfers.
Given a program segment, our aim is to determine the computation and data mapping onto processors. Parallelism can be exploited by transforming the loop nest suitably and then distributing the iterations of the transformed outermost loop onto the processors. The distribution of data onto processors may then result in communication and synchronization which counters the advantages obtained by parallelism. This paper presents an algorithm which results in the optimal performance while simultaneously considering the conflicting goals of parallelism and data locality.
While a programmer can manually write code to enhance data locality by specifying data distribution among processors, we present a technique where we can automatically derive data distribution given the program structure. We present a method by which the program is restructured such that when the outer loop iterations are mapped onto the processors, it results in the least communication. Wherever communication is unavoidable, we restructure the inner loop(s) so that data can be transferred using block transfers; such an approach is referred to as message vectorization.
In this paper, we consider the cases where we allocate outer iterations to processors so that each outer loop iteration is done by a single processor. The data is then allocated so that there is minimum communication and all communication is done through block transfers. This paper deals with an algorithm to restructure the program to enhance data locality while still enabling parallelism. We construct the entries of a legal invertible transformation matrix so that there is a one-to-one mapping from the original iteration space to the transformed iteration space. This transformation when applied to the original loop structure will do the following:
The transformation matrix is derived from
the data reference matrix of the array references.
Given a loop nest with indices 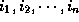 which is
represented by a column vector
which is
represented by a column vector 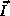 , we define a data reference
matrix,
, we define a data reference
matrix,  , for each array reference A (distinct or non-distinct)
in a loop nest such that the array reference can be written in the
form
, for each array reference A (distinct or non-distinct)
in a loop nest such that the array reference can be written in the
form 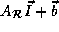 where
where 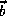 is the offset vector.
is the offset vector.
Example 1:
for i = 1 to 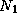 do
for j = 1 to
do
for j = 1 to 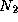 do
for k = 1 to
do
for k = 1 to 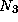 do
do
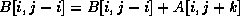
In the above example, the data reference matrix for the array B is
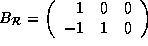 ,
and the data reference matrix for array A is
,
and the data reference matrix for array A is
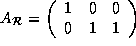 .
Note that there are two data reference matrices for the array B
though they are identical. For each array,
we use only the distinct data reference matrices.
.
Note that there are two data reference matrices for the array B
though they are identical. For each array,
we use only the distinct data reference matrices.
On applying a transformation T to a loop with index I, the
transformed loop index becomes 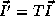 and the
transformed data reference matrix becomes
and the
transformed data reference matrix becomes 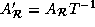 . The columns of
. The columns of  determine the array subscripts of
the references in the transformed loop. The key aspect of the
algorithm presented in this paper is that the entries of the inverse
of the transformation matrix are derived using the data
reference matrices.
determine the array subscripts of
the references in the transformed loop. The key aspect of the
algorithm presented in this paper is that the entries of the inverse
of the transformation matrix are derived using the data
reference matrices.
Li and Pingali [7] discuss the completion of partial transformations derived from the data access matrix of a loop nest; the rows of the data access matrix are subscript functions for various array accesses (excluding constant offsets). Their work assumes that all arrays are distributed by columns. In contrast, our work attempts to find the best distribution for various arrays (by rows, columns, or blocks) such that communication incurred is minimal; for each possible combination of distribution of arrays, we find the best compound loop transformation that results in least communication. Among all these possible distributions (and the associated loop restructuring), we find the one that incurs the smallest communication overhead. Several researchers have addressed the issue of automatic alignment [2,3,4,5,6,8,10]. None of these except [1] addresses the interaction of program transformations and data mapping.
Consider Example 1 above which is similar to the one in
[7]. There are two references to the array B (though not
distinct) and one reference to the array A. Li and Pingali
[7] assume that all arrays are distributed by columns and
derive a transformation matrix that matches column-distribution.
Unlike in [7] the loop can be distributed in such a way
that there is no communication incurred. Both the arrays can be
distributed by rows, i.e., each processor can be assigned an
entire row of array A and an entire row of array B. This makes the
loop run without any communication. We notice that the first row in
the data reference matrix for the arrays A and B are the same
i.e.,  .
This allows the first dimension of both the arrays to be distributed
( i.e., by rows) over the processors so that there is no
communication. In the next section, we derive an algorithm to
construct a transformation matrix, which determines the distribution
of data.
.
This allows the first dimension of both the arrays to be distributed
( i.e., by rows) over the processors so that there is no
communication. In the next section, we derive an algorithm to
construct a transformation matrix, which determines the distribution
of data.
We restrict our analysis to affine array references in loop nests whose upper and lower bounds are affine. We assume that the iterations of the outermost loop are distributed among processors. To exploit data locality and reduce communication among processors, we further look at transformations that facilitate block transfers so that the data elements which are referenced are brought to local memory in large chunks; this allows to amortize the high message start-up costs over large messages. We assume that the data can be distributed along any one dimension of the array (wrapped or blocked). The results can be easily generalized where data is distributed along multiple dimensions and block transfers set up in outer iterations.
Let the array indices of the original loop be
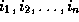 . Let the array indices of the transformed
loop be
. Let the array indices of the transformed
loop be 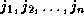 . We look for transformations such
that the LHS array has the outermost loop index as the only element in
any one of the dimensions of the array, e.g.
. We look for transformations such
that the LHS array has the outermost loop index as the only element in
any one of the dimensions of the array, e.g.
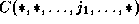 where
where 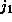 is in the
is in the 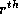 dimension and ``
dimension and `` '' indicates a term independent of
'' indicates a term independent of 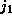 . The LHS
array can then be distributed along dimension r. This means that the
data reference matrix of the transformed array reference C,
i.e.,
. The LHS
array can then be distributed along dimension r. This means that the
data reference matrix of the transformed array reference C,
i.e., 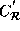 has at least one row which has the first
entry as non-zero and the rest as zero. For all arrays that appear on
the right hand side:
has at least one row which has the first
entry as non-zero and the rest as zero. For all arrays that appear on
the right hand side:
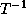 such that one dimension of the RHS has
only the innermost loop index, e.g.
such that one dimension of the RHS has
only the innermost loop index, e.g.
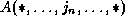 and all the other dimensions are
independent of the innermost loop index (that is, ``
and all the other dimensions are
independent of the innermost loop index (that is, `` '' indicates a
term independent of
'' indicates a
term independent of  ). This allows a block transfer to the local
memory before the execution of the innermost loop. This means that a
row in the transformed data reference matrix
). This allows a block transfer to the local
memory before the execution of the innermost loop. This means that a
row in the transformed data reference matrix  has a
row with all entries zero except in the last column, which is
non-zero. Also, the last column of the
has a
row with all entries zero except in the last column, which is
non-zero. Also, the last column of the  has all
remaining entries as zero.
has all
remaining entries as zero.
Consider the following loop where n is the loop nesting level and d the dimension of the arrays.
forLet the inverse of the transformation matrix beto
do
for
to
do
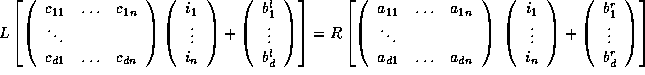
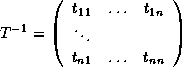 .
Let
.
Let 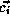 be the
be the 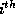 row of the reference matrix of the LHS
array and
row of the reference matrix of the LHS
array and 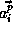 be the
be the 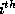 row of the reference matrix
of the
row of the reference matrix
of the 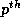 distinct RHS array. Let
distinct RHS array. Let 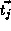 be the
be the
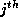 column of
column of 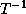 . The algorithm is shown in Figure 1.
. The algorithm is shown in Figure 1.

Figure 1: Algorithm for data distribution and loop transformations
We illustrate the use of the algorithm through several examples in this section. The reader is referred to [9] for a detailed discussion of the algorithm.
Example 2: Matrix Multiplication
for i = 1 to N do
for j = 1 to N do
for k = 1 to N do
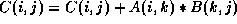
The reference matrices of the arrays are:
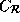 =
= 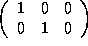 ,
,
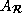 =
= 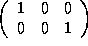 , and
, and
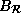 =
= 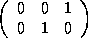 .
.
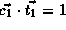 ,
, 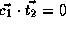 , and
, and
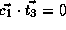 . Therefore we have,
. Therefore we have,
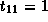 ,
, 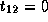 , and
, and 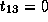 .
.
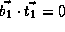 ,
, 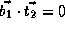 , and
, and 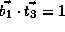 .
Therefore we have,
.
Therefore we have,
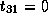 ,
, 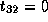 , and
, and 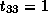 ;
and
;
and 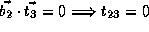 .
Finally we have,
.
Finally we have,
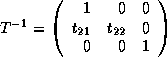 .
For a unimodular transformation,
.
For a unimodular transformation, 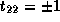 .
Note that dependence vector is
.
Note that dependence vector is 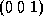 ,
and therefore, there are no constraints on
,
and therefore, there are no constraints on 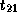 .
This results in the identity matrix as the transformation matrix,
and thus nothing need be done.
Distribute A and C by rows, and B by columns.
The shown next gives the best performance we can get in terms of
parallelism and locality.
.
This results in the identity matrix as the transformation matrix,
and thus nothing need be done.
Distribute A and C by rows, and B by columns.
The shown next gives the best performance we can get in terms of
parallelism and locality.
for u = 1 to N do
for v = 1 to N do
read 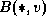 for w = 1 to N
for w = 1 to N
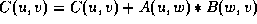
We go ahead and complete the algorithm by
looking at distributing the LHS array in the next dimension.
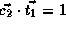 ,
,
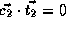 , and
, and
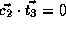 .
Therefore we have,
.
Therefore we have,
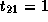 ,
, 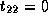 , and
, and 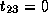 .
.
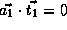 ,
,
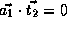 , and
, and
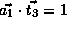 .
Therefore we have,
.
Therefore we have,
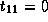 ,
, 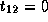 and
and 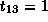 ;
and
;
and 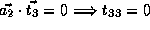 .
.
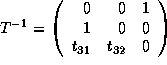 .
For a unimodular transformation,
.
For a unimodular transformation, 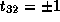 .
Therefore,
.
Therefore,
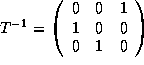 and
and 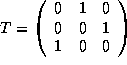 .
Distribute the arrays A, B, and C by columns.
The transformed loop is given below:
.
Distribute the arrays A, B, and C by columns.
The transformed loop is given below:
for u = 1 to N do
for v = 1 to N do
read 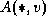 for w = 1 to N do
for w = 1 to N do
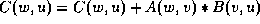
We see that the performance of the loop is similar in both the
cases. Therefore the array C can either be distributed by columns
with the above transformation, or by rows with no transformation
for the same performance with respect to communication.
Consider the SYR2K (from BLAS) example shown below.
Example 3: SYR2K
for i = 1 to N do
for j = i to 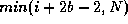 do
for
do
for 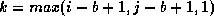 to
to 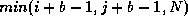 do
do
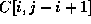 +=
+= 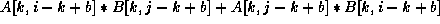
The reference matrices for the arrays are:
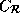 =
= 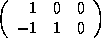 ,
,
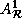 =
= 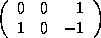 , and
, and 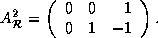 In addition,
In addition, 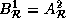 and
and
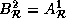 .
.
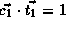 ,
,
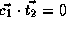 , and
, and
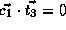 .
Therefore we have,
.
Therefore we have,
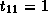 ,
, 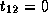 and
and 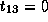 .
.
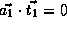 ,
,
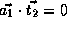 , and
, and
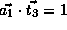 .
We have
.
We have 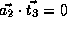 .
Therefore,
.
Therefore,
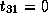 ,
, 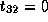 , and
, and 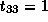 ;
and
;
and
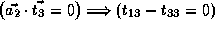 , which is not true.
, which is not true.
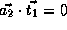 ,
,
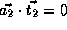 ,
,
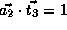 and
and 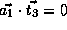 .
Therefore,
.
Therefore,
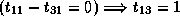 ;
;
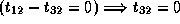 ; and
; and
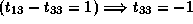 ,
which is not true since
,
which is not true since 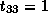 .
Since the reference matrix for array A and B are the same, there can
be no block transfers for B as well.
.
Since the reference matrix for array A and B are the same, there can
be no block transfers for B as well.
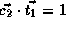 ,
,
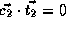 , and
, and
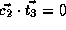 .
Therefore,
.
Therefore,
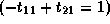
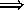
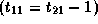 ,
,
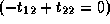
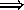
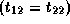 , and
, and
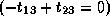
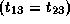 .
.
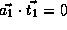 ,
,
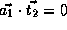 , and
, and
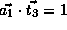 .
Therefore,
.
Therefore, 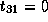 ,
, 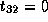 and
and 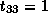 ,
and
,
and 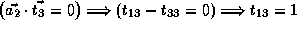 and
and 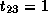 .
.
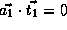 ,
,
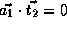 , and
, and
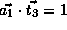 .
Therefore,
.
Therefore, 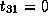 ,
, 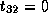 and
and 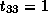 ,
and
,
and 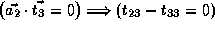 and
and 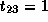 .
.
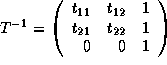 .
Since the reference matrices for B is the same as that of A we
distribute B and A in the same manner.
We choose the unknown values such that
T is a legal unimodular transformation.
A possible
.
Since the reference matrices for B is the same as that of A we
distribute B and A in the same manner.
We choose the unknown values such that
T is a legal unimodular transformation.
A possible 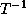 is
is 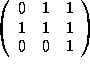 and
and 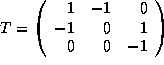 .
The transformed reference matrices are as follows:
.
The transformed reference matrices are as follows:
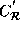 =
= 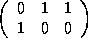 ,
,
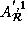 =
= 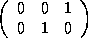 , and
, and 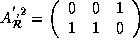 .
Using the above algorithm we distribute the arrays A, B, and
C by columns and the
transformed code with block transfers is as follows:
.
Using the above algorithm we distribute the arrays A, B, and
C by columns and the
transformed code with block transfers is as follows:
for u = 1 to N do for v = u todo read
; read
; read
; read
; for
to
do
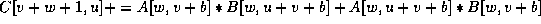
This paper illustrated an algorithm which derives the terms in the transformation matrix which gives the best locality and minimum communication on distributed memory machines. We used the concept of data reference matrices for individual array references. Using this as the starting point, we systematically derived the best set of transformation matrices which give both good locality while enabling parallelism. Unlike [7], where a padding matrix is used along with an arbitrary set of rows in the basis matrix, we generate a transformation matrix systematically. The algorithm also gives an optimal distribution of arrays on to the processors such that block transfers are enabled to reduce inter-processor communication. Here, distribution of data only along one dimension is considered. However complex distributions with more than one distributed dimension can be derived using a simple extension of the above algorithm. Work is in progress in deriving more complex distribution of data and iterations along with tiling.
The first author is supported in part by an NSF Young Investigator Award (CCR--9457768), NSF grant CCR--9210422, and by the Louisiana Board of Regents through contract LEQSF (1991-94)-RD-A-09.
Integrating Data Distribution and Loop Transformations
This document was generated using the LaTeX2HTML translator Version 95 (Thu Jan 19 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -t SIAM Conference on Parallel Processing 1995 -split 0 -no_navigation siampap.tex.
The translation was initiated by J. Ramanujam on Thu Mar 2 20:56:42 CST 1995