PLUTO is an automatic parallelization tool that is based on the polyhedral model. The Polyhedral model is a geometrical representation for programs that utilizes machinery from Linear Algebra and Linear Programming for analysis and high-level transformations. PLUTO transforms C programs from source to source for coarse-grained parallelism and locality simultaneously. The core transformation framework mainly works by finding affine transformations for efficient tiling and fusion, but not limited to it.
Current trends in microarchitecture are increasingly towards larger number of processing elements on a single chip. This has made parallelism and multi-core processors mainstream. The difficulty of programming these architectures to effectively tap the potential of multiple on-chip processing units is a significant challenge. Among several approaches to addressing this issue, one that is very promising but simultaneously very challenging is automatic parallelization. This requires no effort on part of the programmer in the process of parallelization and optimization and is therefore very attractive.
Many compute-intensive applications often spend most of their execution time in nested loops. This is particularly common in scientific and engineering applications. The polyhedral model provides a powerful abstraction to reason about transformations on such loop nests by viewing a dynamic instance (iteration) of each statement as an integer point in a well-defined space called the statement's polyhedron. With such a representation for each statement and a precise characterization of inter or intra-statement dependences, it is possible to reason about the correctness of complex loop transformations in a completely mathematical setting relying on machinery from linear algebra and linear programming. The transformations finally reflect in the generated code as reordered execution with improved cache locality and/or loops that have been parallelized. The polyhedral model is applicable to loop nests in which the data access functions and loop bounds are affine combinations (linear combination with a constant) of the enclosing loop variables and parameters.
Tiling is a key transformation in optimizing for parallelism and data locality. There has been a considerable amount of research into these two transformations. Tiling has been studied from two perspectives: data locality optimization and parallelization. Tiling for locality requires grouping points in an iteration space into smaller blocks (tiles) allowing reuse in multiple directions when the block fits in a faster memory (registers, L1, or L2 cache). Tiling for coarse-grained parallelism involves partitioning the iteration space into tiles that may be concurrently executed on different processors with a reduced frequency and volume of inter-processor communication: a tile is atomically executed on a processor with communication required only before and after execution. One of the key aspects of our transformation framework is to find good ways of performing tiling.
Finding good ways to tile for parallelism and locality directly through an affine transformation framework is the central idea in PLUTO. Our approach is thus a departure from scheduling-based approaches in this field as well as partitioning-based approaches (due to incorporation of more concrete optimization criteria). However, it is built on the same mathematical foundations and machinery. Model-driven empirical optimization and automatic tuning approaches (e.g., ATLAS) have been shown to be very effective in optimizing single-processor execution for some regular kernels like matrix-matrix multiplication. There is considerable interest in developing effective empirical tuning approaches for arbitrary input kernels. Our framework can enable such model-driven or guided empirical search to be applied to arbitrary affine programs, in the context of both sequential and parallel execution. Also, since our transformation system operates entirely in the polyhedral abstraction, it is not just limited to C or Fortran code, but could accept any high-level language from which polyhedral domains can be extracted and analyzed.
Papers
PLUTO is described in the following papers and technical reports:
-
U. Bondhugula, A. Hartono, J. Ramanujam,
and P. Sadayappan,
"A Practical and Automatic Polyhedral Program Optimization System,"
Proc. ACM SIGPLAN 2008 Conference
on Programming Language Design and Implementation (PLDI 08),
Tucson, June 2008.
[
http://dl.acm.org/authorize?N20736
http://dl.acm.org/citation.cfm?id=1375595]
[Extended version: Technical Report]
Abstract: We present the design and implementation of an automatic polyhedral source-to-source transformation framework that can optimize regular programs (sequences of possibly imperfectly nested loops) for parallelism and locality simultaneously. Through this work, we show the practicality of analytical model-driven automatic transformation in the polyhedral model.Unlike previous polyhedral frameworks, our approach is an end-to-end fully automatic one driven by an integer linear optimization framework that takes an explicit view of finding good ways of tiling for parallelism and locality using affine transformations. The framework has been implemented into a tool to automatically generate OpenMP parallel code from C program sections. Experimental results from the tool show very high performance for local and parallel execution on multi-cores, when compared with state-of-the-art compiler frameworks from the research community as well as the best native production compilers. The system also enables the easy use of powerful empirical/iterative optimization for general arbitrarily nested loop sequences.
-
U. Bondhugula, M. Baskaran, S. Krishnamoorthy, J. Ramanujam,
A. Rountev, and P. Sadayappan,
"Automatic Transformations for Communication-Minimized
Parallelization and Locality Optimization in the
Polyhedral Model,"
in Proc. CC 2008 - International Conference on
Compiler Construction,
Budapest, Hungary, March-April 2008.
[pdf]
[pdf]
Abstract: The polyhedral model provides powerful abstractions to optimize loop nests with regular accesses. Affine transformations in this model capture a complex sequence of execution-reordering loop transformations that can improve performance by parallelization as well as locality enhancement. Although a signifi- cant body of research has addressed affine scheduling and partitioning, the problem of automatically finding good affine transforms for communication-optimized coarse-grained parallelization together with locality optimization for the general case of arbitrarily-nested loop sequences remains a challenging problem.
We propose an automatic transformation framework to optimize arbitrarilynested loop sequences with affine dependences for parallelism and locality simultaneously. The approach finds good tiling hyperplanes by embedding a powerful and versatile cost function into an Integer Linear Programming formulation. These tiling hyperplanes are used for communication-minimized coarse-grained parallelization as well as for locality optimization. The approach enables the minimization of inter-tile communication volume in the processor space, and minimization of reuse distances for local execution at each node. Programs requiring one-dimensional versus multi-dimensional time schedules (with schedulingbased approaches) are all handled with the same algorithm. Synchronization-free parallelism, permutable loops or pipelined parallelism at various levels can be detected. Preliminary studies of the framework show promising results.
Performance
Summary of results below are with Pluto git version
114e419014c6f14b3f193726e951b935ad120466 (25/05/2011) on an
Intel Core i7 870 (2.93 GHz), 4 GB DDR3-1333 RAM running Linux
2.6.35 32-bit with ICC 12.0.3. Examples, problem sizes, etc.
are in examples/ dir (or see git examples/ tree). Actual running times (in seconds) are here.
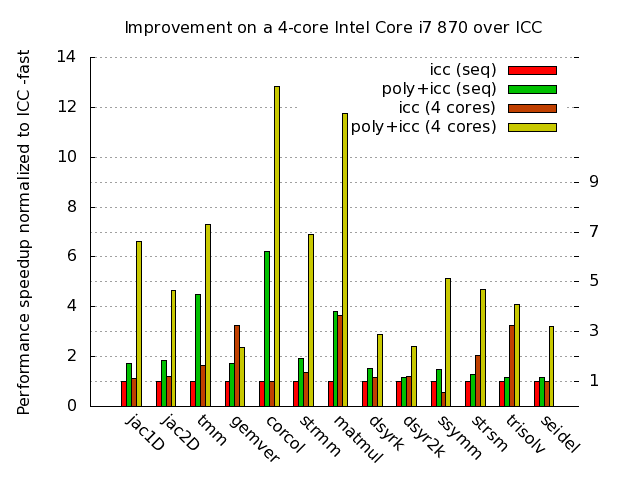
Old
All results below (old) were from a Intel Core2 Quad Q6600 on Linux x86-64 (2.6.18) with ICC 10.1 used to compile original and transformed/parallelized codes. These were from pluto-0.0.1.
Imperfect Jacobi stencil
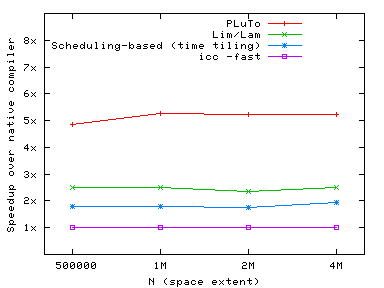
|
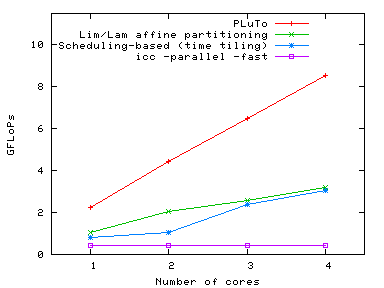
|
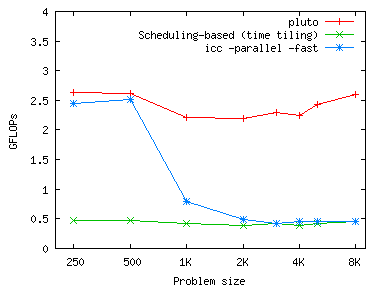
2-d FDTD
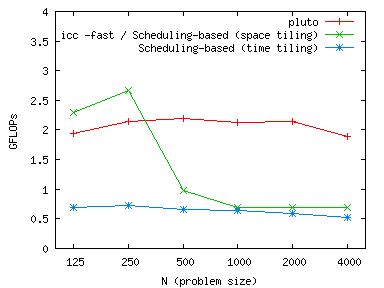
|
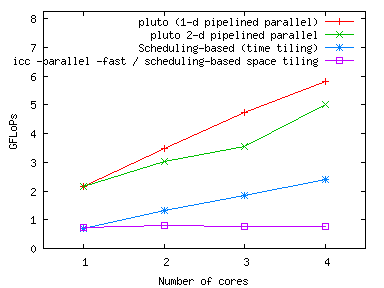
|
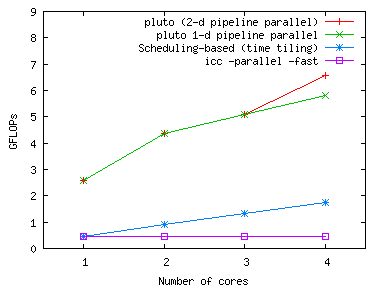
LU decomposition
|
|
GEMVER, Doitgen
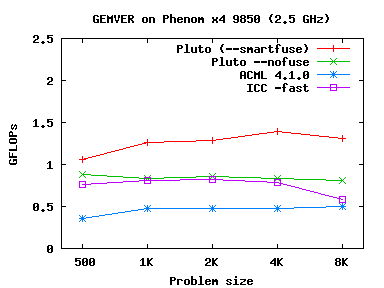
|
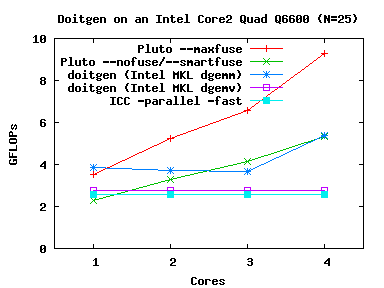
|
DGEMM
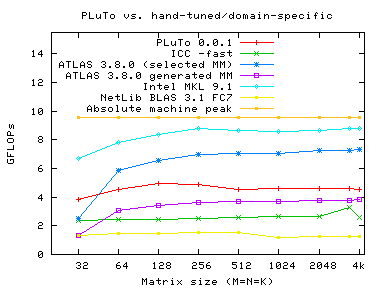
|
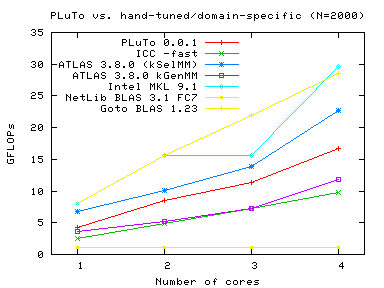
|
ATLAS was tuned with GCC 4.1. kSelMM perf numbers were approximated using the timing report produced after tuning ATLAS ('make time'). kSelMM, kGenMM perf on 2, 3 cores was interpolated (linearly) from perf on 1 and 4 cores.
For addditional details see the PLUTO website.
Funding
This work was supported in part by the National Science Foundation through awards 0121676, 0121706, 0403342, 0508245, 0509442, 0509467, 0541409, 0811457, and 0811781.