where
Subhash Kak
Department of Electrical & Computer Engineering
Louisiana State University
Baton Rouge, LA 70803-5901; kak@ece.lsu.edu
The problem of initializing phase in a quantum computing system is considered. The initialization of phases is a problem when the system is initially present in a superposition state as well as in the application of the quantum gate transformations, since each gate will introduce phase uncertainty. The accumulation of these random phases will reduce the effectiveness of the recently proposed quantum computing schemes. The paper also presents general observations on the nonlocal nature of quantum errors and the expected performance of the recently proposed quantum error-correction codes that are based on the assumption that the errors are either bit-flip or phase-flip or both. It is argued that these codes cannot directly solve the initialization problem of quantum computing.
Keywords: Quantum computing, error-correction, initialization
A quantum state is undetermined with respect to its phase. This indeterminacy is in principle irremovable[8]. The uncertainty of phase, together with superposition, is responsible for the power of quantum mechanics. It also compels us to speak of information in positivist terms--with respect to an observation rather than in an absolute sense.
Since phase indeterminacy is fundamental to quantum description, it is relevant to examine its implications for quantum computation. This indeterminacy can manifest itself in a variety of ways due to the interaction with the environment or while initializing the quantum register. Quantum computing algorithms assume that the state of the quantum register has its phase uncertainty lumped together, so that it can be ignored. This is true enough in certain idealized state preparations. But more realistic situations may not permit it to be lumped together.
Effects of decoherence in the implementation of quantum computation have been widely discussed in the literature[3, 4, 9] as one of its main drawbacks. Random phase shifts, without disentaglement of the states, can also cause serious problems in an ongoing quantum computation. These are unitary transformations of the form:
![]()
where ![]() and
and ![]() contain unknown phase angles.
contain unknown phase angles.
Recent quantum computation algorithms[13, 5] use a method of increasing the amplitude of a marked solution state at the expense of unmarked states. This is achieved by changing the difference in the phase angles of the marked and the unmarked states. But injection of random phases makes it impossible to perform search that will exploit quantum parallelism.
At the implementation level, the representation of a unitary transformation in terms of a sequence of small-degree gates (such as 2-bit gates) will introduce random phase shifts at each gate that will have an effect similar to random phases in a register. In other words, the current conception of quantum computers appears to be unsuitable in terms of implementation.
A quantum register of length n is postulated
where all the superpositions of the ![]() basis states exist with
the amplitudes:
basis states exist with
the amplitudes:
![]()
The idea in the initialization of the quantum register is
to place all the ![]() states in a superposition
where each basis state is equally probable.
But how is this done?
By placing a bit, say a 0, in each cell.
Now, the following transformation
states in a superposition
where each basis state is equally probable.
But how is this done?
By placing a bit, say a 0, in each cell.
Now, the following transformation
![]()
is applied to each bit, transforming it into the
superposition with the amplitudes ![]() .
.
But this would be true only to within an unknown phase angle. Strictly speaking, the state of the cell should be written as:
![]()
where ![]() is the unknown phase of the initial
0.
is the unknown phase of the initial
0.
Such a preparation for each qubit leads to the lumping together of the uncertainty for the state of the register. Here we can imagine that photons have been passed through a horizontal polarizing filter and then rotated by the transformation M to produce superposition qubits.
But to consider this problem from a less idealistic perspective, it should be remembered that the object that carries the qubit, be it a photon, an electron, or an atom or a molecule with a certain spin state, is already physically present at its location. Given that fact, the initialization procedure is to let the object relax to the superposition state which in its most general form will be:
![]()
The state of the quantum register will then be:
![]()
Although each of the ![]() states has the same probability,
the associated phases are unknown and so it is impossible
to use a method of amplitude amplification on any
marked state.
Phase rotation for a case where the phases are randomly
distributed will be meaningless.
states has the same probability,
the associated phases are unknown and so it is impossible
to use a method of amplitude amplification on any
marked state.
Phase rotation for a case where the phases are randomly
distributed will be meaningless.
It is normal to speak of the phase function with the state of the quantum system, but this can also be expressed, equivalently, in terms of an arbitrary phase associated with the unitary operator because, operationally, from the point of view of a measurement, these two are indistinguishable. Clearly, the problem of the initialization of the quantum register will have a parallel in the initialization of the apparatus used to implement unitary transformations.
The quantum computers implements the time-evolution operator U, that represents the transformation on the data in the register, in terms of smaller gates. For example, DiVincenzo[2] showed that two-bit gates are universal for quantum computation. This was done by showing that appropriate sequence of two-bit gates can realize Deutsch's three-gates that implement the Toffoli reversible gates.
But the unitary transformation with each gate, in itself, is associated with an unknown phase, and these values will migrate in the direct product operation used to construct the larger gates. In other words, the realization of the system unitary matrix in terms of the small gates will be correct only in the absence of the random phases. In the recursive development of the S-matrices for the various gates, Deutsch[1] failed to include the unknown phase with the embedded S-terms, assuming thereby that the gates were initialized.
Implementations
of quantum computing based on
trapped ions, quantum dots, cavity-QED, and
nuclear magnetic resonance (NMR) are
being investigated[3].
Here it is assumed that there are no randomized
phases in the initialized register.
But we must consider the
issue of decoherence that leads
to a decay of the superposition of states to a
particular base state due to an interaction with
the environment.
The decoherence time can vary from ![]() sec for
electron-hole excitation in the bulk of a
semiconductor to
sec for
electron-hole excitation in the bulk of a
semiconductor to ![]() sec for nuclear spin
on a paramagnetic atom.
If
sec for nuclear spin
on a paramagnetic atom.
If ![]() is the typical decoherence time, the
decoherence characteristics for a single qubit
are proportional to
is the typical decoherence time, the
decoherence characteristics for a single qubit
are proportional to ![]() .
.
For multiple qubits one must multiply the individual characteristics. For a quantum register of n qubits, the decoherence characteristics are given by
![]()
In other words, the effective decoherence time decreases linearly with the length of the register.
Decoherence may be viewed as a decay in the off-diagonal elements of the density matrix representation of the state of the register. But in operational terms, the process is a cumulative effect of random phase shifts introduced by the interaction with the atoms of the environment. Ultimately, the qubit object falls in one of the basis states in equilibrium with the state function of the environment.
In this perspective, the equilibrium may
be viewed to be the end result of a
walk executed by the phase of each
qubit within the energy state basin
to its least value.
But since the qubits are physically isolated to the
extent possible, one may take this walk to be a random one.
If the step size in this walk is s,
associated with a characteristic time of ![]() ,
then after
,
then after ![]() will be
will be ![]() .
.
Since, the distribution of the random walk can be approximated by the Gaussian function, a Gaussian error with a linearly increasing variance will characterize the departure from the desired values of the phase angles.
To stress why the knowledge of relative phases is
important consider
Grover's quantum search algorithm[5], where
a certain transformation is applied to the state which
computes the property that the database item being searched
uniquely satisfies, marking that state in the process, further generating
transformed
states in superposition.
Next, is the procedure that increases the amplitude of
the marked state progressively: the phase angle of the marked state is rotated through
![]() radians and the diffusion transform D applied as follows:
radians and the diffusion transform D applied as follows:
![]()
This process is repeated a total of about ![]() times
after which the state is measured when it is found in
the marked state with probability close to 1, thus allowing us
to find the database item in about
times
after which the state is measured when it is found in
the marked state with probability close to 1, thus allowing us
to find the database item in about ![]() steps compared
to the average of
steps compared
to the average of ![]() steps in a classical
algorithm.
steps in a classical
algorithm.
In this algorithm, an error of ![]() in the phase of
the marked state will cause a corresponding error
of
in the phase of
the marked state will cause a corresponding error
of ![]() in the amplitude
of the marked state, if it is assumed that the errors
in the phases of the other states cancel out.
in the amplitude
of the marked state, if it is assumed that the errors
in the phases of the other states cancel out.
When N is large, the error in amplitude will be
![]() in each step, but this will progressively increase
in subsequent steps.
in each step, but this will progressively increase
in subsequent steps.
In a classical information system the basic error is represented by a
0 becoming a 1 or vice versa.
The characterization of such errors is in terms of
an error rate, ![]() ,
associated with such flips.
The correction of such errors is achieved by appending
check bits to a block of information bits.
The redundancy provided by the check bits can be
exploited to determine the location of errors using the
method of syndrome decoding.
These codes are characterized by a certain capacity
for error-correction per block.
Errors at a rate less than the capacity of the
code are completely corrected.
,
associated with such flips.
The correction of such errors is achieved by appending
check bits to a block of information bits.
The redundancy provided by the check bits can be
exploited to determine the location of errors using the
method of syndrome decoding.
These codes are characterized by a certain capacity
for error-correction per block.
Errors at a rate less than the capacity of the
code are completely corrected.
Now let us look at a quantum system.
Consider a single cell in a quantum register.
The error here can be due to a random unitary
transformation or by entanglement with the environment.
These errors cannot be defined in a graded sense because
of the group property of unitary matrices
and the many different ways the entanglements
can be expressed.
Let us consider just the first type of error,
namely that of random unitary transformation.
If the qubit is the state ![]() , it can
become
, it can
become
![]() .
Likewise, the state
.
Likewise, the state ![]() can become
can become
![]() .
In the initialization of the qubit a similar
error can occur[7].
If the initialization process consists of collapsing
a random qubit to the basis state
.
In the initialization of the qubit a similar
error can occur[7].
If the initialization process consists of collapsing
a random qubit to the basis state ![]() , the definition
of the
basis direction can itself have a small error associated
with it.
This error is analog and so, unlike error in classical
digital systems, it cannot be controlled.
In almost all cases, therefore, the qubits will have
entangled states, although the level of entanglement
may be very low.
, the definition
of the
basis direction can itself have a small error associated
with it.
This error is analog and so, unlike error in classical
digital systems, it cannot be controlled.
In almost all cases, therefore, the qubits will have
entangled states, although the level of entanglement
may be very low.
From another perspective, classical error-correction codes map the information bits into codewords in a higher dimensional space so that if just a few errors occur in the codeword, their location can, upon decoding, be identified. This identification is possible because the errors perturb the codewords, locally, within small spheres. Quantum errors, on the other hand, perturb the information bits, in a nonlocal sense, to a superposition of many states so the concept of controlling all errors by using a higher dimensional codeword space cannot be directly applied.
According to the positivist understanding of quantum mechanics, it is essential to speak from the point of view of the observer and not ask about any intrinsic information in a quantum state[6]. Let's consider, therefore, the representation of errors by means of particles in a register of N states.
We could consider errors to be equivalent to either n bosons or fermions. Bosons, in a superpositional state, follow the Bose-Einstein statistics. The probability of each pattern will be given by
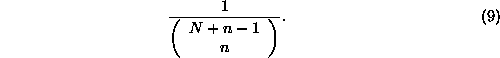
So if there are 3 states and 1 error particle, we can only distinguish
between 3 states: ![]() .
Each of these will have a probability of
.
Each of these will have a probability of ![]() .
To the extent this distribution departs from
that of classical mechanics, it represents nonlocality at
work.
.
To the extent this distribution departs from
that of classical mechanics, it represents nonlocality at
work.
If the particles are fermions, then they are indistinguishable, and with n error objects in N cells, we have each with the probability
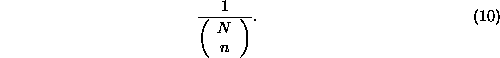
If states and particles have been identified, these statistics will be manifested by a group of particles. If the cells are isolated then their histories cannot be described by a single unitary transformation.
Like the particles, the errors will also be subject to the same statistics. These statistics imply that the errors will not be independent, an assumption that is basic to the error-correction schemes examined in the literature.
To summarize, important characteristics of quantum errors that must be considered are component proliferation, nonlocal effects and amplitude error. All of these have no parallel in the classical case. Furthermore, quantum errors are analog and so the system cannot be shielded below a given error rate. Such shielding is possible for classical digital systems.
We know that a computation need not require any expenditure of energy if it is cast in the form of a reversible process. A computation which is not reversible must involve energy dissipation. Considering conservation of information+energy to be a fundamental principle, a correction of random errors in the qubits by unitary transformations, without any expenditure of energy, violates this principle.
Can we devise error-correction coding for quantum systems? To examine this, consider the problem of protein-folding, believed to be NP-complete, which is, nevertheless, solved efficiently by Nature. If a quantum process is at the basis of this amazing result, then it is almost certain that reliable or fault-tolerant quantum computing must exist but, paying heed to the above-mentioned conservation law, it appears such computing will require some lossy operations.
Every unitary matrix can be transformed by a suitable unitary matrix into a diagonal matrix with all its elements of unit modulus. The reverse also being true, quantum errors can play havoc.
The general unitary transformation representing errors for a qubit is:
![]()
These errors ultimately change the probabilities of the qubit being decoded as a 0 and as a 1. From the point of view of the user, when the quantum state has collapsed to one of its basis states, it is correct to speak of an error rate. But such an error rate cannot be directly applied to the quantum state itself.
Unlike the classical digital case, quantum errors cannot be completely eliminated because they are essentially analog in nature.
The unitary matrix (11) represents an infinite number of cases of error. The error process is an analog process, and so, in general, such errors cannot be corrected. From the point of view of the qubits, it is a nonlocal process.
If it is assumed that the error process can be represented by a small rotation and the initial state is either a 0 or a 1, then this rotation will generate a superposition of the two states but the relative amplitudes will be different and these could be exploited in some specific situations to determine the starting state. But, obviously, such examples represent trivial cases.
The error process may be usefully represented by a process of quantum diffusions and phase rotations.
Shor[11] showed how the decoherence in a qubit could be corrected by a system of triple redundancy coding where each qubit is encoded into nine qubits as follows:
![]()
,
![]()
Shor considers the decoherence process to be one where a qubit decays into a weighted amplitude superposition of its basis states. In parallel to the assumption of independence of noise in classical information theory, Shor assumes that only one qubit out of the total of nine decoheres. Using a Bell basis, Shor then shows that one can determine the error and correct it.
But this system does not work if more than one qubit is in error. Quantum error is analog, so each qubit will be in some error and so this scheme will, in practice, not be useful in completely eliminating errors.
The question of decoherence, or error, must be considered as
a function of time.
One may use the exponential function ![]() as a measure of the decoherence probability of the
amplitude of the qubit.
The measure of decoherence that has taken place by time t
will then be given by the probability,
as a measure of the decoherence probability of the
amplitude of the qubit.
The measure of decoherence that has taken place by time t
will then be given by the probability, ![]() :
:
![]()
In other words, by time t, the amplitude of the
qubit would have decayed to a fraction
![]() of its original value.
At any time t, there is a
of its original value.
At any time t, there is a ![]() chance that the
probability amplitude of the initial state will
be a fraction
chance that the
probability amplitude of the initial state will
be a fraction ![]() of the
initial amplitude.
of the
initial amplitude.
If we consider a rotation error in each qubit through angle ![]() ,
there exists some
,
there exists some ![]() so that the probability
so that the probability
![]()
This means that we cannot represent the qubit error probability by an assumed value p as was done by Shor in analogy with the classical case. In other words, there can be no guarantee of eliminating decoherence.
The recently proposed models of
quantum error-correction codes assume
that the error in the
qubit state ![]() can be either a bit flip
can be either a bit flip ![]() ,
a phase flip between the relative phases of
,
a phase flip between the relative phases of ![]() and
and ![]() , or both [14, 12, 10].
, or both [14, 12, 10].
In other words, the errors are supposed to take the pair of amplitudes (a,b) to either (b,a), (a, -b), or (-b,a).
But these three cases represent a vanishingly small subset of all the random unitary transformations associated with arbitrary error. These are just three of the infinity of rotations and diffusions that the qubit can be subject to. The assumed errors, which are all local, do not, therefore, constitute a distinguished set on any physical basis.
In one proposed error-correction code,
each of
the states
![]() or
or ![]() is represented by
a 7-qubit code, where the
strings of the codewords represent the
codewords of the single-error correcting
Hamming code, the details of which we don't
need to get into here.
The code for
is represented by
a 7-qubit code, where the
strings of the codewords represent the
codewords of the single-error correcting
Hamming code, the details of which we don't
need to get into here.
The code for ![]() has an even number of
1s and the code for
has an even number of
1s and the code for ![]() has an odd number
of 1s.
has an odd number
of 1s.
![]()
![]()
![]()
![]()
As mentioned before, the errors are assumed to be either in terms of phase-flips or bit-flips. Now further ancilla bits-- three in total-- are augmented that compute the syndrome values. The bit-flips, so long as limited to one in each group, can be computed directly from the syndrome. The phase-flips are likewise computed, but only after a change of the bases has been performed.
Without going into the details of these steps, which are a straightforward generalization of classical error correction theory, it is clear that the assumption of single phase and bit-flips is completely artificial.
In reality, errors in the 7-qubit words will generate an superposition state of 128 sequences, rather than the 16 sequences of equations (15) and (16), together with 16 other sequences of one-bit errors, where the errors in the amplitudes are limited to the phase-flips mentioned above. All kinds of bit-flips, as well as modifications of the amplitudes will be a part of the quantum state.
We can represent the state, with the appropriate phase shifts associated with each of the 128 component states, as follows:
![]()
While the amplitudes of the newly generated components will be small, they would, nevertheless, have a non-zero error probability. These components, cannot be corrected by the code and will, therefore, contribute to an residual error probability.
The amplitudes implied by (17) will, for the 16 sequences of the original codeword after the error has enlarged the set, be somewhat different from the original values. So if we speak just of the 16 sequences the amplitudes cannot be preserved without error.
Furthermore, the phase errors in (17) cannot be corrected. These phases are of crucial importance in many recent quantum algorithms.
It is normally understood that in classical systems if error rate is smaller than a certain value, the error-correction system will correct it. In the quantum error-correction systems, this important criterion is violated. Only certain specific errors are corrected, others even if smaller, are not.
In summary, the proposed models are based on a local error model while real errors are nonlocal where we must consider the issues of component proliferation and amplitude errors. These codes are not capable of completely correcting small errors that cause new component states to be created.
The nonlocal nature of the quantum errors is seen clearly in the sensitivity characteristics of these errors.
Consider that some data sets related to a problem are being simultaneously processed by a quantum machine. Assume that by some process of phase switching and diffusion the amplitude of the desired solution out of the entire set is slowly increased at the expense of the others. Nearing the end of the computation, the sensitivity of the computations to errors will increase dramatically, because the errors will, proportionately, increase for the smaller amplitudes. To see it differently, it will be much harder to reverse the computation if the change in the amplitude or phase is proportionally greater.
This means that the ``cost'' of quantum error-correction will depend on the state of the computing system. Even in the absence of errors, the sensitivity will change as the state evolves, a result, no doubt, due to the nonlocal nature of quantum errors. These errors can be considered to be present at the stage of state preparation and through the continuing interaction with the environment and also due to the errors in the applied transformations to the data. In addition, there may exist nonlocal correlations of qubits with those in the environment. The effect of such correlations will be unpredictable.
Quantum errors
cannot be localized. For example,
when speaking of rotation errors, there always exists some
![]() so that
so that ![]() .
.
When doing numerical calculations on a computer, it is essential to have an operating regime that provides reliable, fault-tolerant processing. Such regimes exist in classical computing. But the models currently under examiniation for quantum computing cannot eliminate errors completely. The method of syndrome decoding, adapted from the theory of classical error-correcting codes, appears not to be the answer to the problem of fault-tolerant quantum computing. New approaches to error-correction may be needed.
The undetermined phase of a quantum state can be seen, equivalently, in an undetermined phase associated with each unitary operator. Normally, this has no significance because the usual representations deal with the entire system and so the phase is effectively a lumped term that has no observational value. In considering a unitary transformation as being built out of smaller blocks, the phase cannot be ignored. In other words, there is no simple way we can effectively ``initialize'' each quantum gate.
If one did not concern oneself with the question of the realization of the gates, assuming that the system unitary transformation will be somehow carried out, one still has a difficulty with the random phases in the component states of a quantum register. Given these random phases, one cannot manipulate the amplitudes to increase the value for a marked state as is required in the search problem. If the random phases exist in the initialized register, computations exploiting quantum superposition cannot be performed. If the randomization doesn't exist in the initialized register and is forced upon the computation in the later stages, then this might shorten the time range where useful computations can be performed even more than by decoherence.
We don't know of any simple method to correct for the random phase errors by the use of the proposed quantum error correction codes because these errors will not necessarily be within bounds[10]. Besides, the error-correction systems will be plagued with the same random phase problems that apply to other quantum gates and registers. As mentioned before, it is nonlocality, related both to the evolution of the quantum information system and errors, that makes it difficult for syndrome decoding to work.
How should error-correction be defined then? Perhaps through a system akin to associative learning in spin glasses.
The Initialization Problem in Quantum Computing
This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -link 0 found4.
The translation was initiated by Subhash Kak on Fri Jan 29 18:36:45 CST 1999